NMR coupling constant calculation
NMR analysis is one of the essential techniques for determining the molecular structures of organic compounds. In particular, the vicinal coupling constant 3J, which depends on the dihedral angle around the central bond (between atoms at positions 2 and 3), can be used to predict the three-dimensional structures of organic compounds by applying appropriate formulas and parameters. Recently, it has become possible to predict the three-dimensional structures of proteins and other biopolymers by combining torsion angle information derived from 3J coupling constants with interproton distance data obtained from NMR-NOE measurements. However, as the size of a molecule increases, the number of possible conformational isomers also increases. As the result, the observed coupling constants represent an average over the conformational isomers. Therefore, relying solely on experimental data may lead to the prediction of an 'unnatural' average structure that does not actually exist in reality.
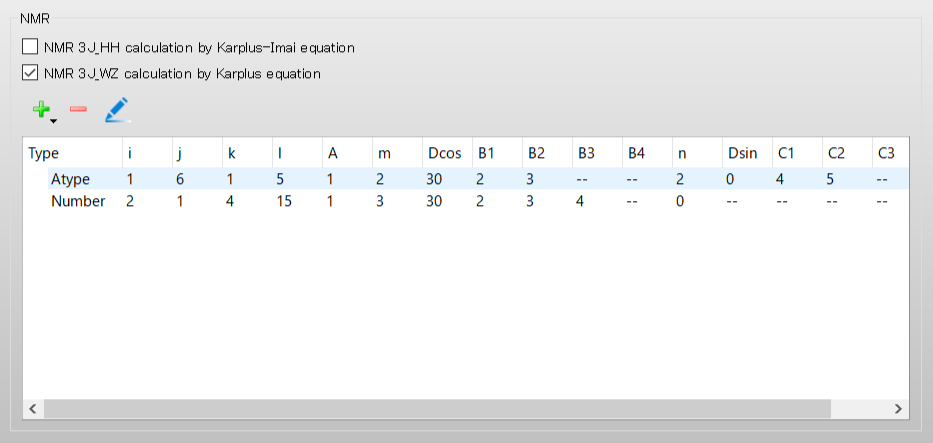
CONFLEX has two types of 3J calculations.
- 3JHH around Csp3-Csp3 bond using Karplus-Imai equation
- 3J for arbitrary combination of four atoms using Karplus equation with user-defined parameters
Furthermore, it is possible to calculate 3J values for each conformer generated through conformation search and to compute their thermodynamic average. By comparing the calculated values with experimental measurements, the molecular state observed in NMR analysis can be inferred. In addition, this approach supports a variety of conformational analyses, such as evaluating steric effects on physical properties and reactivity, as well as enabling more accurate three-dimensional structural analysis.
This chapter provides an overview of NMR coupling constant calculations and explains how to use this function in CONFLEX.
[Vicinal proton-proton coupling constant (3JHH) calculation using Karplus-Imai equation]
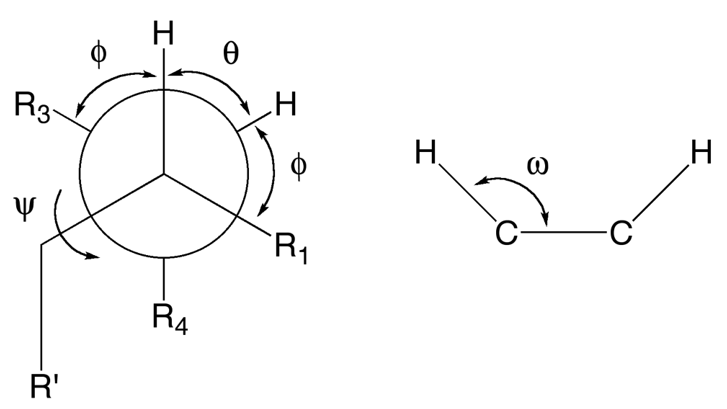
The Karplus–Imai equation (shown below) [1], an improved version of the Karplus equation developed to calculate the vicinal proton–proton coupling constant 3JHH around a Csp3-Csp3 bond, has been implemented in CONFLEX 7 and later versions with the parameter set from reference [1].
The constants and symbols have the following meanings:
| Symbol | Explanation |
|---|---|
| 3JHH | Vicinal coupling constant |
| θ | Dihedral angle between coupling protons |
| Δχi | Difference in group electronegativity between substituent and hydrogen (=2.08) calculated according to Mullay's methods. |
| φi | Dihedral angle between coupling proton and substituent |
| Δχβj | Difference between the Mullay group electronegativity of β-substituents and the average electronegativity of alkanes (=2.40) |
| ψj | Dihedral angle between coupling proton and β-substituent |
| ω1, ω2 | H-C-C bond angle |
| rC-C | C-C bond length |
| r | Distance between coupling proton and nearest atom, excluding directly bonded carbon atoms and α-substituents |
| A-I, K | Constants |
| W, M | Constants varied according to the type of substitution |
| L | Constant varied for the type of nearest atom carbon or oxygen |
For details on the Karplus-Imai equation, please refer to ref. [1]. Generally, the NMR analysis function using the Karplus-Imai equation is based on the 3JHHM method, which is included in the 3JHH2 program [2] published by the Japanese Chemical Program Exchange Organization (JCPE, currently Japan Computer Chemistry Society).
NMR-3JHH calculation of initial and optimized structures
This section explains how to calculate the 3JHH value using 3,3-Dimethyl-1-mercapto-2-butanol as an example.
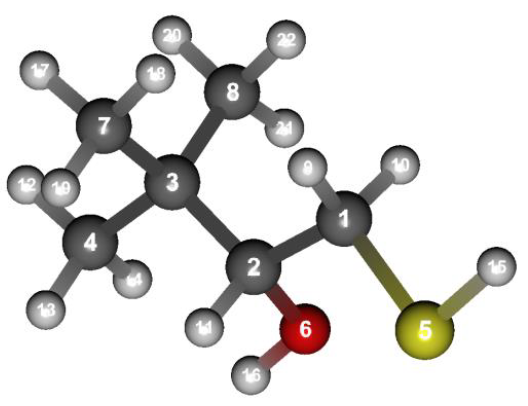
Structure data (DMB.mol)
3,3-DIMETHYL-1-MERCAPTO-2-BUTANOL
22 21 0 0 0 1 V2000
-0.42228 1.47032 -0.03918 C 0 0 0 0 0
0.00590 -0.00052 -0.00318 C 0 0 0 0 0
-0.52383 -0.87942 -1.16021 C 0 0 0 0 0
0.05386 -2.30850 -1.02981 C 0 0 0 0 0
0.14718 2.32958 1.47446 S 0 0 0 0 0
1.43693 -0.05700 0.03175 O 0 0 0 0 0
-2.06329 -0.99499 -1.09495 C 0 0 0 0 0
-0.12896 -0.31902 -2.54213 C 0 0 0 0 0
-1.52983 1.55723 -0.10193 H 0 0 0 0 0
0.01067 1.97322 -0.93329 H 0 0 0 0 0
-0.34401 -0.45530 0.95369 H 0 0 0 0 0
-0.36277 -2.99093 -1.80548 H 0 0 0 0 0
-0.18224 -2.75288 -0.03596 H 0 0 0 0 0
1.16022 -2.32442 -1.15440 H 0 0 0 0 0
-0.32229 3.55489 1.17617 H 0 0 0 0 0
1.68463 -0.92111 0.31239 H 0 0 0 0 0
-2.45015 -1.70017 -1.86565 H 0 0 0 0 0
-2.56803 -0.02106 -1.28092 H 0 0 0 0 0
-2.40160 -1.36949 -0.10193 H 0 0 0 0 0
-0.45439 -1.00120 -3.36038 H 0 0 0 0 0
0.97328 -0.19276 -2.63627 H 0 0 0 0 0
-0.60365 0.66747 -2.74267 H 0 0 0 0 0
1 2 1 0 0 0
1 5 1 0 0 0
1 9 1 0 0 0
1 10 1 0 0 0
2 3 1 0 0 0
2 6 1 0 0 0
2 11 1 0 0 0
3 4 1 0 0 0
3 7 1 0 0 0
3 8 1 0 0 0
4 12 1 0 0 0
4 13 1 0 0 0
4 14 1 0 0 0
5 15 1 0 0 0
6 16 1 0 0 0
7 17 1 0 0 0
7 18 1 0 0 0
7 19 1 0 0 0
8 20 1 0 0 0
8 21 1 0 0 0
8 22 1 0 0 0
M END
[Execution from Interface]
Open the DMB.mol file using CONFLEX Interface.
Select [CONFLEX] from the Calculation menu, and then click in the calculation setting dialog that appears.
A detailed settings dialog will be displayed.

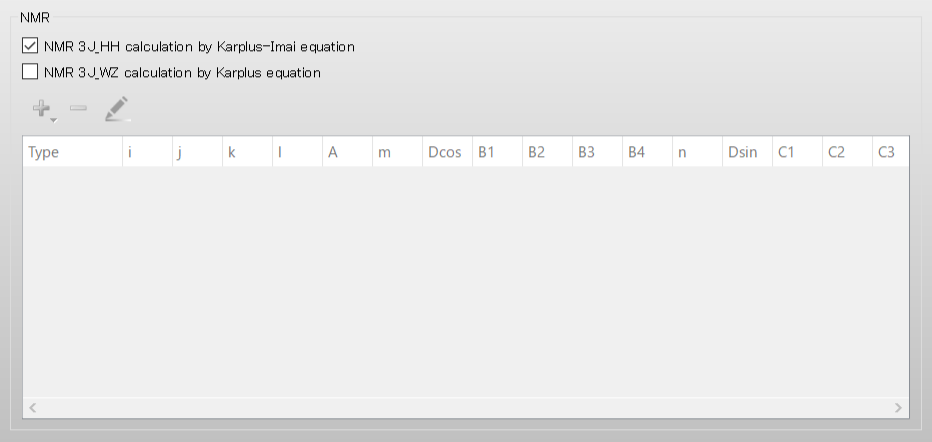
Next, check the [NMR 3J_HH calculation by Karplus-Imai equation] checkbox in the [NMR] dialog of the detailed settings dialog. CONFLEX will automatically determine all possible coupled proton pairs.
The calculation of the 3JHH value is applied to the optimized structure. If you want to apply the calculation to the initial structure, select [No Optimization] from the [Optimization Method:] pull-down menu in the [Geometry Optimization] dialog.
After completing the calculation settings, click to start the calculation.
[Execution from command line]
The calculation settings are defined by specifying keywords in the DMB.ini file.
DMB.ini file
NMR
[NMR] keyword is used to calculate the 3JHH value using the Karplus-Imai equation. CONFLEX automatically determines all possible coupled proton pairs.
The 3JHH value calculation is applied to the optimized structure. If you want to apply the calculation to the initial structure, add [OPT=NONE] to the DMB.ini file.
DMB.ini file
NMR OPT=NONE
Store the two files of DMB.mol and DMB.ini in a single folder, and execute the following command to start the calculation.
C:\CONFLEX\bin\conflex-10a.exe -par C:\CONFLEX\par DMBenter
The command above is for Windows OS. For other OS, please refer to [How to execute CONFLEX].
Calculation results
CONFLEX provides a file with the nmr extension that contains the results of the NMR 3J calculation. The 3JHH calculation results for the initial structure of 3,3-Dimethyl-1-mercapto-2-butanol are shown below (DMB.nmr). In this case, the 3JHH for two proton pairs around the C1–C2 bond are calculated: H9 and H10 are bonded to C1, and H11 is bonded to C2 (3JH9H11 and 3JH10H11).
In the first part of the output, the Karplus-Imai equation and the parameters used in this equation are displayed. In the following section, titled “3JHHM TABLES:”, the serial numbers of the coupled proton pairs (in the “HI” and “HJ” columns) to be calculated are shown.
!====================================================================================! ! ! ! NMR-3JHHM: VICINAL H-H COUPLING CONSTANTS CALCULATION ! ! ! !------------------------------------------------------------------------------------! ! ! ! DATE: 2021/02/08 TIME: 12:47:34.37 ! ! DMB: 3,3-DIMETHYL-1-MERCAPTO-2-BUTANOL ! ! EMPIRICAL FORMULA: C6H14OS MW = 134.077 ! ! FORCE FIELD: MMFF94S(2010-12-04HG) ! ! ! !------------------------------------------------------------------------------------! ! ! ! 3JHHM (KARPLUS-IMAI) EQUATION FORMULA: ! ! 3JHH = P1*COS(A) + P2*COS(2*A) + P3*COS(3*A) + P4*COS(2*A)*COS(2*A) + ! ! C1*[ P5*ELENEG*COS(A)*COS(B) + P6*ELENEG*COS(2*B) + P7*ELENEG ] + ! ! P8*(ANGLE - 110.0) + P9*(LENGTH - 1.5) + P10*E(BETA)*|COS(2*C)| + ! ! P11/R(C)**4 + P12/R(O)**4 + CONSTANT ! ! ! ! ! ! PARAMETERS: ! ! P1 P2 P3 P4 P5 P6 ! ! -1.2246 5.0935 -0.1055 0.5711 0.8319 0.0433 ! ! P7 P8 P9 P10 P11 P12 ! ! 0.0345 -0.2058 -8.9222 0.1438 -8.9395 6.9202 ! ! ! ! MONO 1,1-DI 1,2-DI TRI TETRA ! ! WEIGHT 1.0000 2.5500 1.1600 2.2900 1.4000 ! ! CONSTANT 7.5075 7.0306 6.4793 6.5432 5.5319 ! ! ! !------------------------------------------------------------------------------------! ! ! ! 3JHHM TABLES: ! ! ! ! NUMBER OF CENTRAL BONDS HAVING VICINAL COUPLING PROTONS: 1 ! ! LIST OF COUPLING PROTON PAIRS AND CENTRAL BONDS: ! ! COUPLED NO HI I J HJ ! ! ---------- ------------------- ------------------- ! ! 1 9 1 2 11 ! ! 2 10 1 2 11 ! ! -------------------------------------------------- ! ! ! !====================================================================================! ! TOTAL NUMBER OF CONFORMERS FOUND: 1 ! ! TEMPERATURE: 298.15 KELVIN ! !=====================================================================================
In the second part of the output, the 3JHH values (in the “3JHH” column) and the internal coordinates around the proton pair for each conformer, which are necessary for the calculation, are displayed under the section “GEOMETRICAL PARAMETERS OF EACH CONFORMER:”. If there are multiple proton pairs around the same C-C bond, the average value of these pairs is also provided (3JHH (AV.) =) in the section “AVERAGED VICINAL H-H COUPLING CONSTANTS:”.
!=====================================================================================================================! ! ! GEOMETRICAL PARAMETERS OF EACH CONFORMER: ! ! NO. CONF ID ENERGY DISTRIB I-J BOND LENGTH H-H PAIR 3JHH PHI ANGLE !---------------------------------------------------------------------------------------------------------------------! ! 1 -------- 36.8731 100.0000 1 - 2 1.5323 9 - 11 2.010 -66.928 110.758 108.891 ! 1 -------- 36.8731 100.0000 1 - 2 1.5323 10 - 11 10.063 173.879 110.105 108.891 !=====================================================================================================================! !====================================================================================! ! ! ! AVERAGED VICINAL H-H COUPLING CONSTANTS: ! ! ! ! 3JHH ( 1 ) = 2.010 (Hz) ! ! 3JHH ( 2 ) = 10.063 (Hz) ! ! 3JHH ( AV. ) = 6.036 (Hz) ! ! ! !====================================================================================!
Note that the results obtained from the NMR 3JHH calculation using an MMFF94s optimized structure may be insufficient, as the parameters of the Karplus-Imai equation are based on the MM2 force field. Therefore, the results of the 3JHH calculation obtained from optimized structures using the EMM2 force field are likely to be more accurate. When performing the NMR 3JHH calculation using EMM2 optimization, you can run CONFLEX as described below.
[Execution from Interface]
Select [EMM2] from the [Force Field:] pull-down menu in the [Force Field] dialog of the detailed settings dialog.
[Execution from command line]
You should create the DMB.ini file that contains the [EMM2] keyword.
DMB.ini file
NMR EMM2
The nmr file obtained from the EMM2 calculation is shown below.
!=====================================================================================================================! ! ! GEOMETRICAL PARAMETERS OF EACH CONFORMER: ! ! NO. CONF ID ENERGY DISTRIB I-J BOND LENGTH H-H PAIR 3JHH PHI ANGLE !---------------------------------------------------------------------------------------------------------------------! ! 1 ----- 12.1470 100.0000 1 - 2 1.5420 9 - 11 1.785 -69.875 110.048 ! 1 ----- 12.1470 100.0000 1 - 2 1.5420 10 - 11 9.573 170.843 109.734 !=====================================================================================================================! !====================================================================================! ! ! ! AVERAGED VICINAL H-H COUPLING CONSTANTS: ! ! ! ! 3JHH ( 1 ) = 1.785 (Hz) ! ! 3JHH ( 2 ) = 9.573 (Hz) ! ! 3JHH ( AV. ) = 5.679 (Hz) ! ! ! !====================================================================================!
NMR-3JHH calculation of multiple conformational isomers
The NMR 3JHH calculation can be combined with a conformational search. Here, we use β-D-glucose as an example.
Steric structure of β-D-Glucose
Structure data of β-D-Glucose (b-D-glucose.mol)
b-D-glucose
24 24 0 0 0 1 V2000
1.3695 0.2061 0.1154 O 0 0 0 0 0
1.2178 -1.0943 0.6579 C 0 0 0 0 0
-1.0088 0.3669 -0.2565 C 0 0 0 0 0
0.3824 0.4861 -0.8691 C 0 0 0 0 0
-2.0178 0.5729 -1.2448 O 0 0 0 0 0
-2.4798 -1.0576 0.9937 O 0 0 0 0 0
-0.2327 -2.5652 1.8842 O 0 0 0 0 0
0.6403 1.8795 -1.4228 C 0 0 0 0 0
2.2841 -1.1000 1.6064 O 0 0 0 0 0
-0.1084 -1.2465 1.3563 C 0 0 0 0 0
-1.2097 -1.0083 0.3471 C 0 0 0 0 0
-0.2182 2.1250 -2.5390 O 0 0 0 0 0
1.4145 -1.8634 -0.1200 H 0 0 0 0 0
-1.1510 1.1467 0.5281 H 0 0 0 0 0
0.5017 -0.2533 -1.6973 H 0 0 0 0 0
-2.8280 0.2840 -0.8591 H 0 0 0 0 0
-2.5257 -1.8924 1.4288 H 0 0 0 0 0
0.4375 -2.6616 2.5390 H 0 0 0 0 0
1.6888 1.9818 -1.7842 H 0 0 0 0 0
0.4468 2.6616 -0.6552 H 0 0 0 0 0
2.8280 -0.3665 1.3741 H 0 0 0 0 0
-0.1927 -0.5339 2.2095 H 0 0 0 0 0
-1.1998 -1.7977 -0.4398 H 0 0 0 0 0
-1.0984 1.9144 -2.2779 H 0 0 0 0 0
1 2 1 0 0 0
1 4 1 0 0 0
2 9 1 0 0 0
2 10 1 0 0 0
2 13 1 0 0 0
3 4 1 0 0 0
3 5 1 0 0 0
3 11 1 0 0 0
3 14 1 0 0 0
4 8 1 0 0 0
4 15 1 0 0 0
5 16 1 0 0 0
6 11 1 0 0 0
6 17 1 0 0 0
7 10 1 0 0 0
7 18 1 0 0 0
8 12 1 0 0 0
8 19 1 0 0 0
8 20 1 0 0 0
9 21 1 0 0 0
10 11 1 0 0 0
10 22 1 0 0 0
11 23 1 0 0 0
12 24 1 0 0 0
M END
[Execution of Interface]
Open the b-D-glucose.mol file using CONFLEX Interface.
Select [CONFLEX] from the Calculation menu, and then click in the calculation setting dialog that appears. A detailed settings dialog will be displayed.

Next, in the [General Settings] dialog of the detailed settings dialog, select [Conformation Search] from the [Calculation Type:] pull-down menu.
Next, check the [NMR 3J_HH calculation by Karplus-Imai equation] checkbox in the NMR dialog.
After completing the calculation settings, click to start the calculation.
CONFLEX first performs a conformation search and then calculates the NMR 3JHH value for each conformer found. It also provides coupling constants weighted by their population probabilities.
[Execution from command line]
The calculation settings are defined by specifying keywords in the b-D-glucose.ini file.
b-D-glucose.ini file
NMR CONFLEX
[NMR] specifies the calculation of 3JHH values using the Karplus-Imai equation.
[CONFLEX] specifies the execution of a conformation search.
Store the two files of b-D-glucose.mol and b-D-glucose.ini in a single folder, and execute the following command to start the calculation.
C:\CONFLEX\bin\conflex-10a.exe -par C:\CONFLEX\par b-D-glucoseenter
The command above is for Windows OS. For other OS, please refer to [How to execute CONFLEX].
CONFLEX first performs a conformation search and then calculates the NMR 3JHH value for each conformer found. It also provides coupling constants weighted by their population probabilities.
Calculation results
When the 3JHH calculation is applied to multiple conformers, the 3JHH values and the internal coordinate information for multiple proton pairs in each conformation are output, along with the thermodynamic averages based on the Boltzmann distribution.
Excerpt from the b-D-glucose.nmr file
... !=====================================================================================================================! ! ! GEOMETRICAL PARAMETERS OF EACH CONFORMER: ! ! NO. CONF ID ENERGY DISTRIB I-J BOND LENGTH H-H PAIR 3JHH PHI ANGLE !---------------------------------------------------------------------------------------------------------------------! ! 1 00000001 79.8320 49.0347 2 - 10 1.5376 13 - 22 8.078 171.796 111.222 110.519 ! 3 - 4 1.5395 14 - 15 9.471 -176.573 109.804 109.384 ! 3 - 11 1.5300 14 - 23 9.059 170.407 109.839 110.494 ! 4 - 8 1.5350 15 - 19 4.390 -67.989 108.838 110.176 ! 4 - 8 1.5350 15 - 20 9.133 174.032 109.247 110.993 ! 10 - 11 1.5257 22 - 23 8.829 -169.298 110.301 110.781 !---------------------------------------------------------------------------------------------------------------------! ! 2 00000002 79.8625 46.5768 2 - 10 1.5353 13 - 22 8.164 173.410 111.296 110.739 ! 3 - 4 1.5385 14 - 15 9.351 -171.357 110.368 109.897 ! 3 - 11 1.5309 14 - 23 8.720 167.539 109.812 110.347 ! 4 - 8 1.5342 15 - 19 0.616 67.424 109.939 112.095 ! 4 - 8 1.5342 15 - 20 3.173 -53.305 108.931 110.080 ! 10 - 11 1.5238 22 - 23 8.935 -169.970 110.281 110.564 !---------------------------------------------------------------------------------------------------------------------! ! 3 00000009 81.7252 2.0081 2 - 10 1.5352 13 - 22 8.211 173.300 111.147 110.580 ! 3 - 4 1.5390 14 - 15 9.396 -172.203 110.326 109.893 ! 3 - 11 1.5318 14 - 23 8.705 167.362 109.759 110.273 ! 4 - 8 1.5341 15 - 19 0.634 67.748 109.885 112.066 ! 4 - 8 1.5341 15 - 20 3.185 -52.960 108.922 110.141 ! 10 - 11 1.5247 22 - 23 8.835 -169.118 110.310 110.552 !---------------------------------------------------------------------------------------------------------------------! ! 4 00000003 81.9524 1.3687 2 - 10 1.5354 13 - 22 8.094 172.342 111.443 110.626 ! 3 - 4 1.5362 14 - 15 9.320 -174.765 110.457 110.531 ! 3 - 11 1.5312 14 - 23 8.887 169.039 109.858 110.365 ! 4 - 8 1.5368 15 - 19 8.184 -169.220 109.281 110.569 ! 4 - 8 1.5368 15 - 20 2.477 69.460 109.957 111.922 ! 10 - 11 1.5245 22 - 23 8.865 -169.387 110.255 110.616 !---------------------------------------------------------------------------------------------------------------------! ...
!====================================================================================! ! ! ! AVERAGED VICINAL H-H COUPLING CONSTANTS: ! ! ! ! 3JHH ( 1 ) = 8.122 (Hz) ! ! ! ! 3JHH ( 2 ) = 9.411 (Hz) ! ! ! ! 3JHH ( 3 ) = 8.890 (Hz) ! ! ! ! 3JHH ( 4 ) = 2.572 (Hz) ! ! 3JHH ( 5 ) = 6.082 (Hz) ! ! 3JHH ( AV. ) = 4.327 (Hz) ! ! ! ! 3JHH ( 6 ) = 8.880 (Hz) ! ! ! !====================================================================================!
It is also possible to perform the 3JHH calculation on the conformers obtained from a previously performed conformation search.
[Execution from Interface]
Store the fxf file obtained from the previously performed conformation search, along with the input file used in the search, in a single folder. For example, store the b-D-glucose.mol and b-D-glucose.fxf files in the same folder. Next, open the b-D-glucose.mol file using the CONFLEX Interface.

Select [CONFLEX] from the Calculation menu, and then click in the calculation setting dialog that appears.
A detailed settings dialog will be displayed.

Next, in the [General Settings] dialog of the detailed settings dialog, select [Conformation Search] from the [Calculation Type:] pull-down menu.

Next, check the [NMR 3J_HH calculation by Karplus-Imai equation] checkbox in the NMR dialog.

When completing the calculation settings, click .
Add [NOSEARCH] keyword to the dialog that appears.
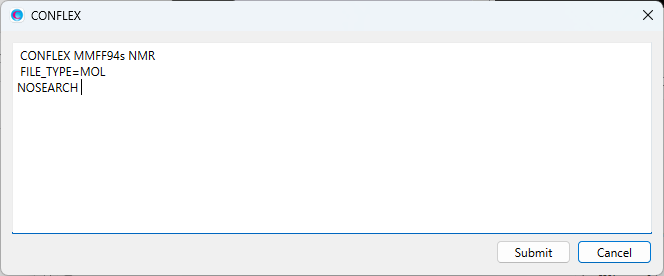
By including both the keywords “CONFLEX” and “NOSEARCH”, the structure data of the conformers is obtained from the fxf file, and new or additional conformational search is not performed. After completing the calculation settings, click to start the calculation.
CONFLEX calculates the NMR 3JHH values for each conformer obtained from the fxf file. Additionally, it provides coupling constants weighted by their existence probabilities.
[Execute by command line]
Store the fxf file obtained from the previously performed conformation search, along with the input file used in the search, in a single folder. For example, store the b-D-glucose.mol and b-D-glucose.fxf files in the same folder. The contents of the b-D-glucose.ini file are shown below.
b-D-glucose.ini file
NMR CONFLEX NOSEARCH
When both the “CONFLEX” and “NOSEARCH” keywords are specified, the structure data of conformers is extracted from the fxf file without performing any new or additional conformation searches.
Execute the following command to start the calculation.
C:\CONFLEX\bin\conflex-10a.exe -par C:\CONFLEX\par b-D-glucoseenter
The command above is for Windows OS. For other OS, please refer to [How to execute CONFLEX].
CONFLEX calculates the NMR 3JHH values for each conformer obtained from the fxf file. Additionally, it provides coupling constants weighted by their existence probabilities.
[3J coupling constant calculation using Karplus equation and customized parameters]
In the previous section, the coupling constants 3JHH were calculated using the Karplus-Imai equation based on the dihedral angle and bond angle, with automatic extraction of H-Csp3-Csp3-H from the structural information. On the other hand, there are many different combinations of 3J values used in NMR structural analysis. Therefore, it would be useful to calculate other 3J values using the Karplus equation and link them with the conformation search.
In CONFLEX8.C and later, it is possible to calculate the 3JWZ value for any combination of four bonded atoms W-X-Y-Z by setting the parameters based on Eq. (1).
where the A, Bm, and Cn are parameters, the θ is the dihedral angle of W-X-Y-Z, and the δcos and δsin are the phase angles of cosine and sine terms, respectively. These parameters can be specified either by the atom type number of MMFF94s (using keyword “NMR_3J_ATYPE =”) or by the serial number of the input data (using keyword “NMR_3J_NUMBER =”). Both methods can be used simultaneously, however, if the parameter set for W-X-Y-Z is defined by both keywords, the specification using the serial number takes precedence.
Conformation search and 3J calculation of β-D-Glucose
We use β-D-Glucose as an example.
Steric structure of β-D-Glucose

Here, we calculate 3JCH of Csp3-Osp3-Csp3-H (Representation by atom types in MMFF94s: 1-6-1-5) using Eq. 2.
Here, the first term of Eq. 2, 1.0, corresponds to the first term of Eq. 1, A. The cosine functions correspond to the second term of Eq. 1 (m=2,B1=2.0,B2=3.0,δcos=30.0). The sine functions correspond to the third term of Eq. 1 (n=2,C1=4.0,C2=5.0,δsin=0.0).
Although the 2-1-4-15 in the serial number corresponds to Csp3-Osp3-Csp3-H combination, we calculate the 3JCH of 2-1-4-15 using Eq. 3.
Eq. 3 corresponds to Eq. 1 with A=1.0, m=3, B1=2.0, B2=3.0, B3=4.0, and δcos=30.0.
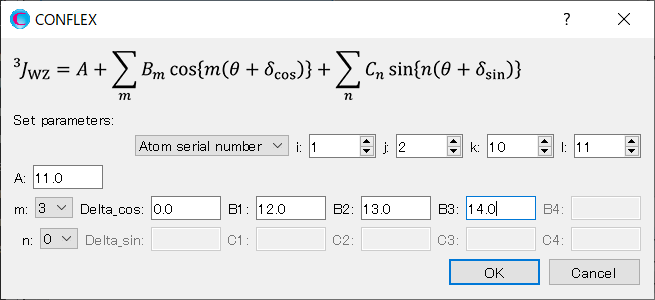
Furthermore, we calculate 3JO1C11 of O1-C2-C10-C11 (Representation by serial number:1-2-10-11) using Eq. 4.
Eq. 4 corresponds to Eq. 1 with A=11.0, m=3, B1=12.0, B2=13.0, B3=14.0, and δcos=0.0.
[Execution from Interface]
Open the b-D-glucose.mol file using CONFLEX Interface.

Select [CONFLEX] from the Calculation menu, and then click in the calculation setting dialog that appears.
A detailed settings dialog will be displayed.

First, in the [General Settings] dialog in the detailed settings dialog, select [Conformation Search] from the [Calculation Type:] pull-down menu.

Next, we configure the settings for the eqs. 2 ~ 4.
Check the [NMR 3J_WZ calculation by Karplus equation] checkbox in the NMR dialog. A dialog for setting the equation will be displayed.
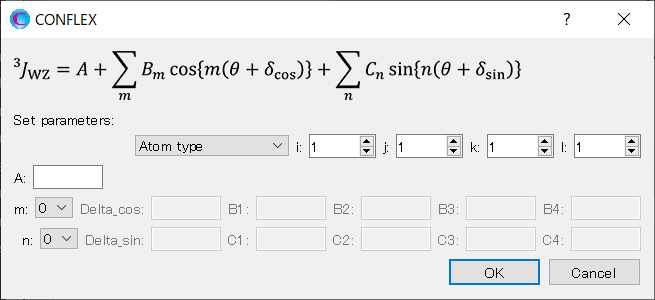
We set up Eq. 2. Select [Atom type] from the [Set parameters:] pull-down menu. Set the i, j, k, and l to 1, 6, 1, and 5, respectively, and set the A to 1.0.
Next, select 2 from the pull-down menu for [m:]. Set the Delta_cos to 30.0. Set the B1 and B2 to 2.0 and 3.0, respectively.
And then, select 2 from the pull-down menu for [n:]. Set the Delta_sin to 0.0. Set the C1 and C2 to 4.0 and 5.0, respectively.
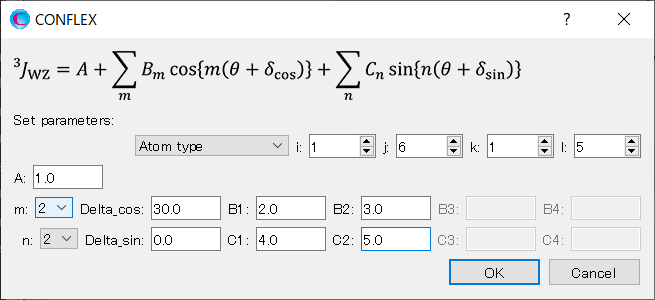
When completing the settings, click .
You can see the parameters for Eq. 2 in the NMR dialog.
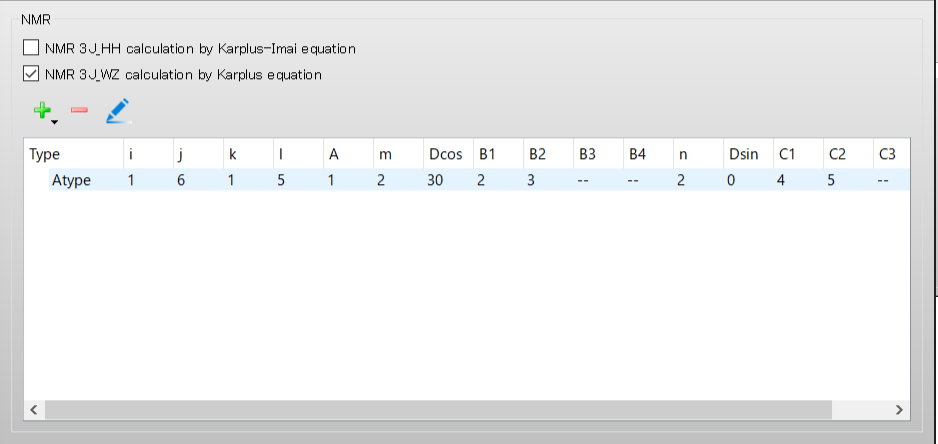
Next, to configure the settings for Eq. 3, click [+]. The dialog for setting the equation will be displayed again.
We set up Eq. 3. Select [Atom serial number] from the [Set parameters:] pull-down menu. Set the i, j, k, and l to 2, 1, 4, and 15, respectively, and set the A to 1.0.
Select 3 from the pull-down menu for [m:]. Set the Delta_cos to 30.0. Set the B1, B2, and B3 to 2.0, 3.0, and 4.0, respectively.
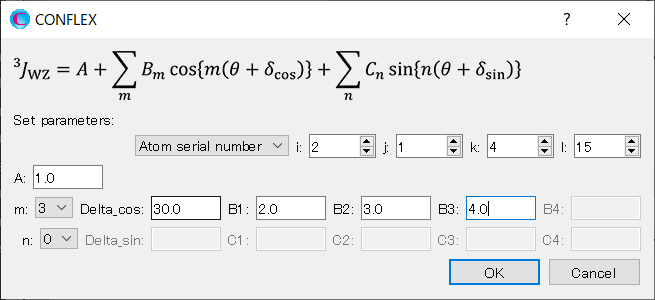
When completing the settings, click .
You can see the parameters for Eq. 3 in the NMR dialog.
Next, to configure the settings for Eq. 4, click [+]. The dialog for setting the equation will be displayed.
We set up Eq. 4. Select [Atom serial number] from the [Set parameters:] pull-down menu. Set the i, j, k, and l to 1, 2, 10, and 11, respectively, and set the A to 11.0.
Select 3 from the pull-down menu for [m:]. Set the Delta_cos to 0.0. Set the B1, B2, and B3 to 12.0, 13.0, and 14.0, respectively.
When completing the settings, click .
You can see the parameters for Eq. 4 in the NMR dialog.
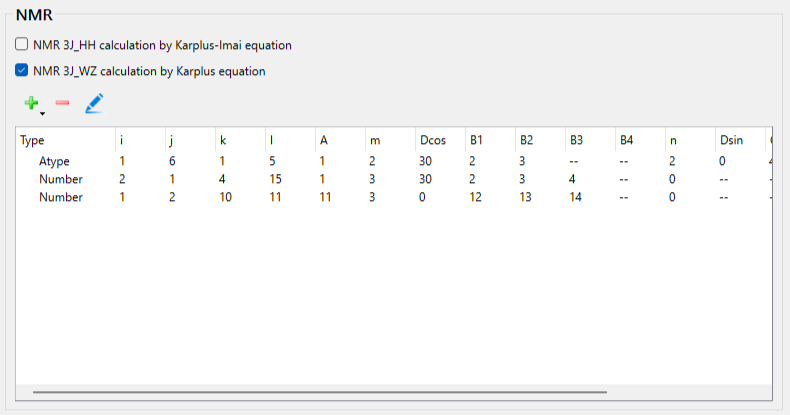
When completing all the settings, click .
CONFLEX will first perform a conformation search and calculate the NMR 3J value of each conformer found using the defined equations.
It also provides coupling constants weighted by an existence probability.
[Execution from command line]
The calculation settings are defined by specifying keywords in the b-D-glucose.ini file.
b-D-glucose.ini file
CONFLEX NMR NMR_3J_ATYPE=(1,6,1,5)(1.0)(COS,30.0,2,2.0,3.0)(SIN,0.0,2,4.0,5.0) NMR_3J_NUMBER=(2,1,4,15)(1.0)(COS,30.0,3,2.0,3.0,4.0) NMR_3J_NUMBER=(1,2,10,11)(11.0)(COS,0.0,3,12.0,13.0,14.0)
For the [NMR_3J_ATYPE=] and [NMR_3J_NUMBER=] keywords, the black text specifies [W-X-Y-Z], the red text specifies the A of Eq. 1, the blue text specifies the second term of Eq. 1, and the green text specifies the third term of Eq. 1.
The parentheses in blue represents (COS,δcos,m,B1,B2,...,Bm), and the parentheses in green represents (SIN,δsin,n,C1,C2,...,Cn). These keywords at lines 3, 4, and 5 set up Eqs. 2, 3, and 4, respectively.
Store the two files of b-D-glucose.mol and b-D-glucose.ini in a single folder, and execute the following command to start the calculation.
C:\CONFLEX\bin\conflex-10a.exe -par C:\CONFLEX\par b-D-glucoseenter
The command above is for Windows OS. For other OS, please refer to [How to execute CONFLEX].
CONFLEX will first perform a conformation search and calculate the NMR 3J value of each conformer found using the defined equations. It also provides coupling constants weighted by an existence probability.
Calculation results
The contents of the b-D-glucose.nmr file obtained from the calculation are shown below. At the beginning of the file, information about the calculated molecule and the Karplus equation is provided.
!====================================================================================!
! !
! NMR 3J COUPLING CONSTANTS CALCULATION !
! !
!------------------------------------------------------------------------------------!
! !
! DATE: 2019/10/02 TIME: 10:49:25.87 !
! BGLU: b-glucose.mol !
! EMPIRICAL FORMULA: MW = 180.063 !
! FORCE FIELD: MMFF94S(2010-12-04HG) !
! !
!------------------------------------------------------------------------------------!
! !
! CALCULATION USING KARPLUS EQUATION FORMULA AS BELOW: !
! !
! 3JWZ = A0 + SUM_I {B_I*COS(I*(D + P_COS))} !
! + SUM_J {C_J*SIN(J*(D + P_SIN))} !
! !
! D : DIHEDRAL ANGLE OF W-X-Y-Z !
! P_COS : PHASE ANGLE FOR COS !
! P_SIN : PHASE ANGLE FOR SIN !
! !
...
Next, the file shows the parameters of Eq. 2 and the atom members to which Eq. 2 is assigned.
! ! ! *** SETTING PARAMETERS BY ATOM TYPES *** ! ! ! ! NO. 1: ATOM TYPES OF DIHEDRAL= 1 - 6 - 1 - 5 ! ! ! ! *** PARAMETER SET *** ! ! ! ! A0 : 1.00000 ! ! ! ! COS PART, P_COS(DEGREE)= 30.00 ! ! I B_I ! ! 1 2.000 ! ! 2 3.000 ! ! ! ! SIN PART, P_SIN(DEGREE)= 0.00 ! ! J C_J ! ! 1 4.000 ! ! 2 5.000 ! ! ! ! ASSIGNED DIHEDRAL: INPUT NO. 4 - 1 - 2 - 13 ! ! ASSIGNED DIHEDRAL: INPUT NO. 2 - 1 - 4 - 15 ! ! ! ...
Next, the file shows the parameters of Eqs. 3 and 4 and the atom members to which each equation is respectively assigned.
In this case, the C2-O1-C4-H15 was already defined using Eq. 2 (see above). Therefore, the program outputs the message "THEN OVERWRITE THE PARAMETERS AS BELOW." and applies Eq. 3 to the C2-O1-C4-H15 instead.
! ! ! *** SETTING PARAMETERS BY INPUT NO. *** ! ! ! ! INPUT NO.: 2 - 1 - 4 - 15 ! ! ! ! CHECK CONNECTIVITY ... EXISTED. ! ! ! ! *** BUT ALREADY SETTING BY ABOVE ATOM TYPES (NO. 1)!!! *** ! ! *** THEN OVERWRITE THE PARAMETERS AS BELOW. *** ! ! ! ! *** PARAMETER SET *** ! ! ! ! A0 : 1.00000 ! ! ! ! COS PART, P_COS(DEGREE)= 30.00 ! ! I B_I ! ! 1 2.000 ! ! 2 3.000 ! ! 3 4.000 ! ! ! ! INPUT NO.: 1 - 2 - 10 - 11 ! ! ! ! CHECK CONNECTIVITY ... EXISTED. ! ! ! ! *** PARAMETER SET *** ! ! ! ! A0 : 11.00000 ! ! ! ! COS PART, P_COS(DEGREE)= 0.00 ! ! I B_I ! ! 1 12.000 ! ! 2 13.000 ! ! 3 14.000 ! ! ! ...
Next, the 3J value, dihedral angle, and contribution of each term in Karplus equation for each conformer are shown.
!------------------------------------------------------------------------------------! ! TOTAL NUMBER OF CONFORMERS FOUND: 15 ! ! TEMPERATURE: 298.15 KELVIN ! !=====================================================================================================================! ! ! GEOMETRICAL PARAMETERS OF EACH CONFORMER: ! ! NO. CONF ID ENERGY DISTRIB X-Y BOND LENGTH W-Z PAIR 3JWZ PHI A0 COS SIN !---------------------------------------------------------------------------------------------------------------------! ! 1 00000001 79.8320 49.0347 1 - 2 1.4198 4 - 13 5.532 62.88 1.000 -3.085 7.618 ! 1 - 4 1.4357 2 - 15 4.533 -59.05 1.000 3.533 0.000 ! 2 - 10 1.5376 1 - 11 -1.380 56.72 11.000 -12.380 0.000 !---------------------------------------------------------------------------------------------------------------------! ! 2 00000002 79.8625 46.5768 1 - 2 1.4181 4 - 13 5.528 62.92 1.000 -3.086 7.615 ! 1 - 4 1.4425 2 - 15 3.334 -62.81 1.000 2.334 0.000 ! 2 - 10 1.5353 1 - 11 -2.574 58.48 11.000 -13.574 0.000 !---------------------------------------------------------------------------------------------------------------------! ! 3 00000009 81.7252 2.0081 1 - 2 1.4184 4 - 13 5.593 62.23 1.000 -3.069 7.662 ! 1 - 4 1.4435 2 - 15 3.655 -61.81 1.000 2.655 0.000 ! 2 - 10 1.5352 1 - 11 -2.237 57.96 11.000 -13.237 0.000 !---------------------------------------------------------------------------------------------------------------------! ...
The thermodynamic average based on the Boltzmann distribution is shown at the end of the file.
!====================================================================================! ! ! ! AVERAGED VICINAL W-Z COUPLING CONSTANTS: ! ! ! ! 3J_WZ ( 1 ) = 5.531 (Hz) ! ! ! ! 3J_WZ ( 2 ) = 3.938 (Hz) ! ! ! ! 3J_WZ ( 3 ) = -1.968 (Hz) ! ! ! !====================================================================================!
References
- “An Extension of multiparametric Karplus equation”, Keisuke Imai, Eiji Ōsawa, Tetrahedron Lett., Vol. 30, No. 32, 4251-4254 (1989).
- “3JHH2”, Keisuke Imai, Eiji Ōsawa, JCPE, P012.